1. Floating Point (부동소수점)
- 아주 크거나 아주 작은 정수 이외 숫자 표현 방법

부동소수점의 장점: 0을 적게 쓸 수 있음 (메모리 절약)
** C에서는 float와 double 로 부동 소수점 나타냄
1) normalized form
e.g., 00500에서
5 앞에 00은 필요 없는 0
필요 없는 0들 뒤에 존재하는 최초의 숫자 5 뒤에 점 찍기.
-> 이진 표현이라면 항상 1
2) 이진 표현

1.xxx -> significand (유효숫자)
.xxx -> fraction
yyy -> exponent
2. Floating Point Standard
- IEEE 표준 754-1985에 의해 정의됨
- 과학적 코드의 이식성 문제를 해결하기 위해 표준 개발됨
- 2가지 표현방식
1) Single precision 단정밀도 (32-bit)
2) Double precision 배정밀도 (64-bit)
3. IEEE Floating-Point Format

s = sign bit (0 = +, 1 = -)
1) normalize significand의 유효범위

- 정규화된 significand는 항상 소수점 앞에 1을 가지므로 저장 필요 x
1 -> hidden bit
2) exponent는 실제 지수에 bias 더한 값으로 저장됨
-> 지수가 항상 양수로 표현되도록 보장하기 위해
single의 bias = 127 -> 2^7 - 1 = 255의 반
double의 bias = 1023 -> 2^10 -1
4. Single-Precision Range
- exponent 00000000 이랑 11111111 은 특수 지수?넘버?
- 00000000: 0을 나타냄
- 11111111: 무한대 or NaN (Not a Number) 나타냄
1) 가장 작은 값
- exponent: 00000001 -> 실제값 = 1 - 127 = -126
- fraction: 000 ... 00 -> significand: 1.0
2) 가장 큰 값
- exponent 11111110 -> 실제값 = 254 - 127 = +127
- fraction: 111 ... 11 -> significand = 약 2.0
** 결정적인 오차는 fraction에서 발생
** 십진수로 변환하면 약 7자리 정도의 유효 숫자 significand 제공 -> 대략 7자리 이후부터 오차 발생
5. Double-Precision Range
마찬가지로 exponent 000...00 이랑 111....11 따로 빼둠
1) 가장 작은 값
- exponent: 00000000001 -> 실제값 = 1 - 1023 = -1022
- fraction: 000..00 -> significand = 1.0
2) 가장 큰 값
- exponent: 11111111110 -> 실제값 = 2046 - 1023 = +1023
- fraction: 111..11 -> significand = 약 2.0
** 대략 16자리부터 오차 발생
6. Floating point precision
상대 relative 정밀도 (fraction이 얼마나 많은 십진수를 정확하게 표현할 수 있는지)
1) single precision
single의 fraction은 23비트
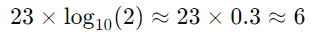
약 6자리 십진수 정밀도
2) Double precision
double의 fraction은 52비트
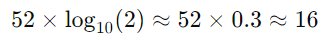
약 16자리 십진수 정밀도
3) Floating point로 변환하는 법
(1) 십진수의 절대값 -> 이진수로 변환
a. 정수 부분 이진수로 기록
b. 소수 부분에 2 곱하기
c. 결과의 정수 부분을 이진수로 기록
d. 소수 부분이 0이 될 때까지 반복
e.g.
0.75를 floating point로
a. 정수는 0
b. 소수 0.75 * 2 = 1.5
c. 정수 부분은 '1', 소수는 0.5
d. 소수 0.5 * 2 = 1.0
e. 정수는 '1', 소수는 '0'
f. 0.11
(2) 식 세우기
e.g. -0.75 = (-1)^1 * 1.1 * 2^-1
(3) exponent에 bias 더하기
single은 127, double은 1023

4) Foating-point를 10진수로 변환하는 방법

fraction 0100..0 -> significand 1.01
** 이진수를 십진수로 변환하는 법
1.01 = 1 * 2^0 + 0 * 2^-1 + 1 * 2^-2 = 1.25
5. Floating Point Addition
1) 4-digit decimal example
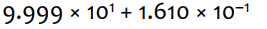
(1) 지수 정렬
더 작은 지수를 큰 지수에 맞추기

(2) significand 더하기
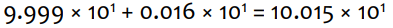
(3) Normalize result & check for over/underflow

(4) Round and renormalize if necessary

6. FP Adder Hardware
much more complex than integer adder
7. FP의 중요성
1. 과학적 코드에서 매우 중요
2. 일상적인 소비자 사용에서도 중요 (e.g, 금융시스템 은행 잔고 오차!?)
3. 인텔 펜티엄 FDIV 버그
-> 부동소수점 나눗셈 연산의 하드웨어 버그
8. 결론
1) 비트 자체는 의미를 지니지 않으며, 그 해석은 적용된 명령에 따라 달라진다.
e.g., 같은 비트 패턴이 정수, 부동 소수점 수, 문자 데이터 등으로 다르게 해석될 수 있음
2) 컴퓨터의 숫자 표현 범위와 정밀도는 제한된다.
3) 프로그램을 작성할 때 이러한 제한을 고려하고, 적절한 오류 처리와 오차를 관리해야 한다.
4) ISA의 산술 연산 지원 - 실제 수를 근사하여 FP로 표현
5) 제한된 range와 precision -> overflow or underflow 발생 가능
6) MIPS ISA의 가장 자주 쓰이는 54개 핵심 명령어가 SPECINT 100%와 SPECFP 97% 커버 (정수, FP 연산 벤치마크)
-> 기타 명령어는 덜 자주 사용됨.
