[LA] Matrix Decomposition

1. Determinant

Laplace expansion = 3*3 matrix의 determinant를 2*2 matrix의 determinant로 정의할 수 있다.

det(A) != 0 -> A is invertible (역행렬 존재x)

det(AB) = det(A)det(B)

det(A) = det(AT)

det(A^-1) = 1/det(A)

 

2. Trace

matrix의 diagonal 다 더한 형태

tr(A + B) = tr(A) + tr(B)

 

det(A) = eigenvalue들의 곱셉

tr(A) = eigenvalue들의 덧셈

 

3. Cholesky Decomposition

A = L LT

for a symmetric, positive definite (all eigenvalues > 0) matrix A, A = LLT

L = lower-triangular matrix with positive diagonals

such L is unique, called Cholesky factor of A

 

det(A) = det(L)det(LT) = det(L)^2

det(L) = multiplication of diagonal entries

det(A) = multiplication of (diagonal entries)^2

 

4. Diagonal Matrix

1. EVD (EigenValue Decomposition)

계산하기 매우 간편 -> 일반 matrix도 diagonal matrix와 비슷하게 만들 수 없을까? -> diagonalizable

 

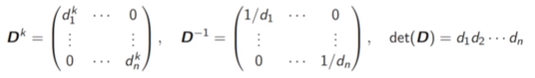
if A is symmetric -> A is orthogonally diagonalizable

if A is symmetric

1) the eigenvalues are all real

2) the eigenvectors to different eigenvalues are perpendicular

A = PDPT

 

그렇다면 symmetric 아닌 matrix는?????

 

2. SVD (Singular Value Decomposition)

EVD는 symmetric에만 적용 가능하지만, SVD는 전부 적용 가능

S = AT A is always symmetric, positive semidefinite.

S에 대해서 EVD를 하는 것!!

A = USVT

AT A = VDVT